Estimación del efecto del distanciamiento social sobre la epidemia de COVID-19 de otoño-invierno en el área metropolitana de Buenos Aires

The international spread of the 2019 novel coronavirus disease (COVID-19) originated in Wuhan, China, has now reached Argentina ¹. The first case of COVID-19 in Latin America was confirmed by Brazil on February 25, 2020 ², and Argentina verified its case-index on March 5. The burden imposed on the region by the COVID-19 spread constitutes an additional challenge for local healthcare systems and economies.
Recent Chinese experience showed that the COVID-19 death rate increases 6-fold in those over 70, and up to 11-fold in those over 80 ³. Since the metropolitan area of Buenos Aires is the largest urban conglomerate in the country with a high population density, and nearly 10% of its inhabitants are over 70 years old, this local scenario constitutes a potential target to explore the impact of the COVID-19 outbreak.
Forecasting the extent of the domestic health risk of epidemics by mathematical modeling is a useful tool for evaluating the feasibility of policies for controlling outbreaks ⁴.
At present, most published simulation-based analyses for COVID-19 come from China, Korea ^5-11, and recently the UK12.These studies have included deterministic mathematical models10, stochastic transmission dynamic prototypes involving international travelers ⁵, and epidemiological analysis based on the Boltzmann function ⁹, and some of them have evaluated government control policies and large-scale public health interventions ⁷.
Recommendations to control an epidemic involve a combination of social distancing measures as hospitalization of symptomatic patients and asymptomatic positive cases or contacts, banning of public events, partial of total lockdown, household self-isolation of the entire population, and school and university closures ^13-14. These measures are principally expected to reduce the peak healthcare demand and mortality rate of COVID-19. However, some concerns exist on the capacity of these interventional strategies to slow down or stop disease transmission, and particularly their social acceptability and economic viability in low- and middle-income countries ¹⁵.
The objective of this study was to develop a timedependent dynamic simulation model to forecast the COVID-19 autumn-winter outbreak in the metropolitan area of Buenos Aires, and to assess the effect of social distancing on epidemic spread.

Material and methods

In this study, we used the Stella software (v9.0.2, High Performance Systems, Hanover, NH) to develop a dynamic stochastic transmission model able to analyze different epidemiological scenarios of potential outbreaks of COVID-19 in the metropolitan area of Buenos Aires. The model used was the ‘Susceptible-Exposed-Infectious-Recovered or Removed’ (SEIR) framework which incorporated appropriate compartments relevant to interventions such as quarantine, isolation and treatment. The model stratified the population into susceptible (S), exposed (E), infectious with symptoms (I), infectious but asymptomatic (A), hospitalized (H) and recovered (R) compartments, with further stratification to include quarantined susceptible (Sq), and isolated exposed (Eq) compartments, as illustrated in Figure 1. Due to the lack of local estimates, the model was parameterized using mostly Tang et al ^8,16 prototype data developed for the Wuhan outbreak.
The current model estimated the cumulative number of COVID-19 cases, the severity of clinical presentation, and the cumulative number of deaths. In addition, we modeled several potential governmental interventions, namely social distancing, to reduce the outbreak spread. A sensitivity analysis was performed to explore the effect of quarantine suspension on the evolution of the total number of symptomatic cases. A steady-state solution was approached in the long run for certain scenarios. Model input data, parameters and assumptions are presented in Table 1.
The series of values obtained from sequential simulations were expressed as means assuming normal distribution. When a range of values was present, parameters were included in the model as normal-distributed or random uniform probabilities between the minimum and maximum extremes of each parameter. Consequently, these stochastic simulations generated plots with visually sawtooth wave time courses. For numerical analysis purposes, the Runge-Kutta 2nd order method was used to solve the differential equations generated in the model. It must be acknowledged that the equations’ solution may differ with the method used, since differences were found when using either Euler or 4th order Runge-Kutta approaches.
The SEIR compartmental model was adapted and formulated with the following system of equations (parameter notation and values are shown in Table 1), as previously described by Tang et al. ^8,16:
S’ = -(βc(t)+c(t)q(1-β))S(I+A)+ λSq
E’ = βc(t)(1-q)S(I+A)-σE
I’ = σ E – (δI(t)+α+γI)I
A’ = σ(1 – )E – γAA
S’q = (1 – β)c(t)qS(I + A) – λSq
E’q = βc(t)qS(I + A) – δqEq
R’ = γII + γAA + γHH
with contact rate c(t) as a decreasing function of time t, given by:
c(t) = (c0 – cb )e-r1t + cb
where c0 is the contact rate at the initial time (i.e. March 20, 2020), cb is the minimum contact rate under the current control strategies, and r1is the exponential decrease of the contact rate. Similarly, δI(t) is set as an increasing function of time t, and equivalently, the period of diagnosis 1/δI(t) is a decreasing function of t described by the following equation:
1/δI(t) = (1/δI0 – 1/δIf)e-r2t + 1/δIf
where, δI0 is the diagnosis rate at the initial time, δIf is the fastest diagnosis rate, and r2 is the exponential decreasing rate.

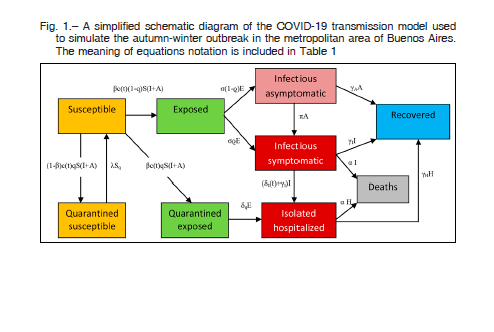
We only modeled the sustained human to human transmission of COVID-19 in the metropolitan area of Buenos Aires over a 5-month time perspective with epidemic curve, beginning on March 20, 2020 with cumulatively observed 93 infected persons, the same day the Argentine government decreed the total and mandatory quarantine. The Metropolitan area of Buenos Aires included the urban agglomeration comprising the city of Buenos Aires and the adjacent 33 districts in the province of Buenos Aires. For comparative purposes, a lowintervention scenario was used, only including 2-week isolation for international travelers and their contacts. The rest of the intervention scenarios also included mandatory quarantine for most of the population and the country’s lockdown. The model simulation was based on the following assumptions: (1) the whole population was susceptible; (2) unprotected contact between the susceptible and the infected would lead to infection;(3) infected people could be asymptomatic or symptomatic; (4) positive cases of asymptomatic COVID-19 were considered non-sick; (5) the intervention was considered to start on March 20, 2020; and (6) a time-dependent stochastic dynamic model was employed.

Results

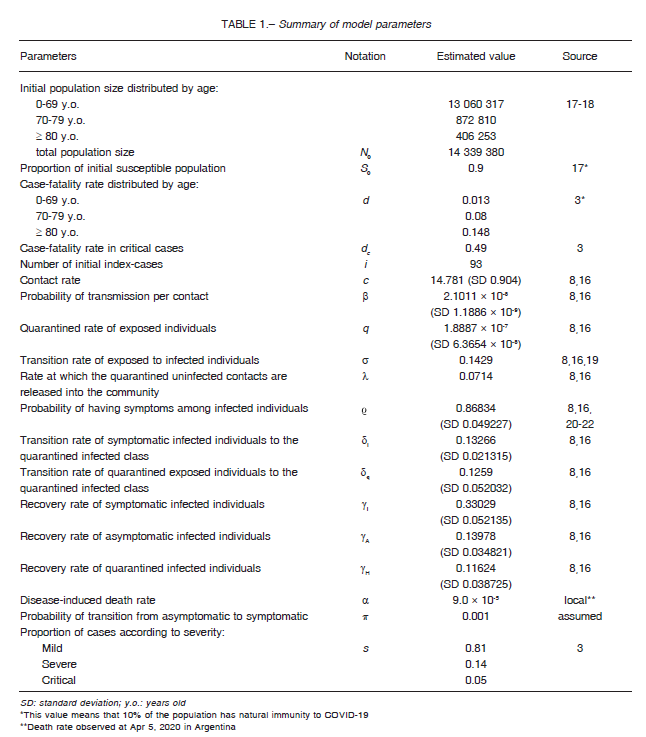
The hypothetical evolution of the cumulative number of symptomatic cases of COVID-19 expected for a 5-month period in the metropolitan area of Buenos Aires according to different levels of intervention measures, namely percent of quarantined population, is shown in Figure 2.
Provided that the quarantine was maintained during the 5-month period, the curve of cases flattened and receded as the proportion of quarantined individuals increased. The maximum peak was expected to appear between May 8 and Jul 8 depending on the quarantine strategy, and the average number of infectious symptomatic cases were 46 840, 30 494, 23 164, 16 179, and 13 196 when 10%, 20%, 30%, 40%, and 50% of the population remained in a 5-month-term continuous quarantine, respectively. The same peak calculated for the low-intervention scenario averaged 88 210 cases between May 1 and May 12.
Regarding the evolution of the cumulative number of COVID-19 cases according to clinical severity, the simulation demonstrated mean values of 81.3%, 14.0%, and 4.7% for mild, severe, and critical clinical presentation of cases, respectively. Figure 3 summarizes the expected cumulative number of critically-ill patients requiring intensive care settings in the metropolitan area of Buenos Aires according to the proportion of quarantined population. In this case, the average number of critical patients at the maximum peak was 2111, 1486, 1173, 858, and 456 when 10%, 20%, 30%, 40%, and 50% of the population remained in quarantine, respectively. The total number of expected deaths for the same simulations averaged 1035, 729, 575, 421, and 224, respectively.
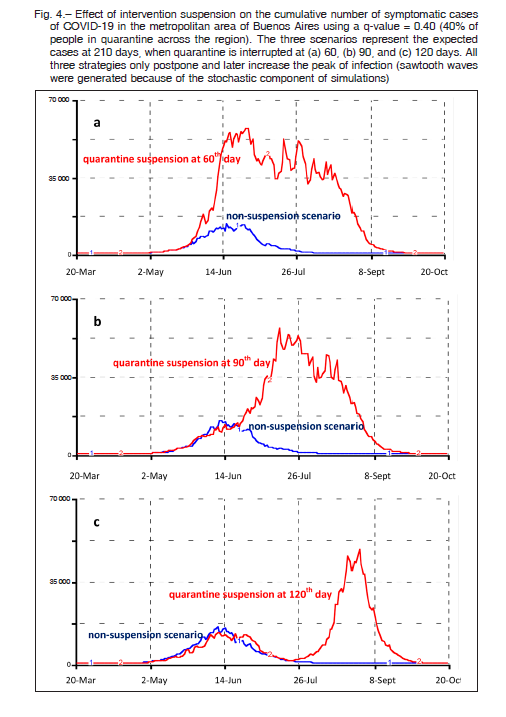
The effect of the end of quarantine on the cumulative number of symptomatic patients considering 40% of people in quarantine across the region is shown in Figure 4. The three scenarios represent the expected cases when quarantine is interrupted after 60, 90, and 120 days of the initial measure implantation (quarantine start day March 20). All three strategies only postpone and later increase the peak of infection. The upper curve of each panel originates from the initial quarantine scenario at 60, 90, and 120 days and near triplicates the peak of infection. These rebounds are due to the exposure of new susceptible individuals who left the quarantine. In this case, simulations were performed at a 210-day term to better appreciate the secondary peak of infection.

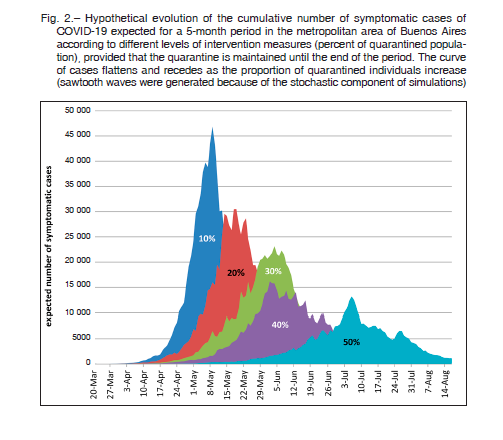
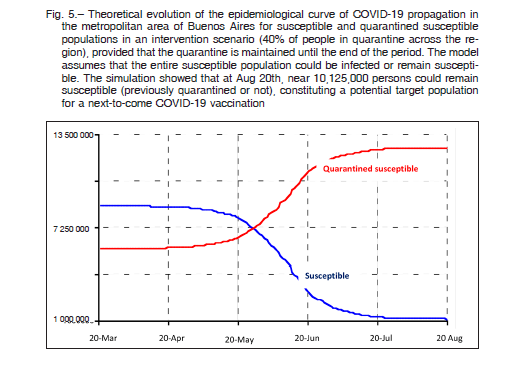
Figure 5 shows the evolution of the theoretical epidemiological curve of COVID-19 propagation in the metropolitan area of Buenos Aires for susceptible and quarantined susceptible populations in an intervention scenario (40% of people in quarantine across the region), provided the quarantine is maintained until the end of the period. The model assumes that the entire susceptible population could be infected or remain susceptible. The simulation shows that at August 20, nearly 10 125 000 persons could remain susceptible (previously quarantined or not), constituting a potential target population for a next-to-come COVID-19 vaccine. Since the quarantined population will remain susceptible in the long term, the simulation revealed a tail of infection extending for more than one year of follow-up (data not shown).

Discussion

In the context of the COVID-19 epidemic in Argentina, estimating the usefulness of social intervention measures to prevent and control a large-scale outbreak plays a key role for evidence-based decisions performed by health policy-makers. Until now, only a few mathematical models have been publicly released to assess population health interventions during the current epidemic ^5-11. We have adapted and implemented a recently published model to estimate the potential short- and mid-term evolution of the COVID-19 outbreak in the metropolitan area of Buenos Aires ^8,16. As a whole, the model considered both symptomatic and asymptomatic forms of the disease, the quarantine of healthy individuals who had contact with COVID-19 positive people, the mandatory quarantine due to the country’s lockdown, the hospitalization of the most severe cases, and the recovery and death rates.
Notwithstanding government interventions involve a combination of public health actions, we particularly used the percentage of individuals on household quarantine to measure the impact of social distancing to avoid contacts and control the outbreak. Similarly, the decision to break the quarantine and expose still susceptible people to normal social life might involve a serious risk of contagion.
In the current study, different levels of quarantine rate useful to reduce transmission-effective contacts were simulated for the whole population of the metropolitan area of Buenos Aires. Model-based estimates showed that for instance, a quarantine of 40 to 50% of the population would be able to produce a 5 to 7-fold decrease in the number of symptomatic cases with respect to the low-intervention scenario, provided that the quarantine was maintained during the full 5-month period. Conversely, the simulation demonstrated that the end of quarantine after two or three months of lockdown initiation would only delay the transmission of the infection, with a late secondary peak of almost a similar number of cases as seen in the lowintervention scenario. In the example shown in Figure 4, after a sudden interruption of the quarantine at the 60th or 90th day, new peaks were expected to appear immediately; while for the 120th day suspension the rebound appeared up to 30 days later.

It has been recognized that the COVID-19 pandemic will actually produce, enough severe illness to overwhelm the health care infrastructure in every country ²³. Since most of the susceptible population is going to be infected sooner or later, independently of intervention measures, the main purpose of implementing temporary social distancing during the COVID-19 outbreak is flattening the contagion curve to avoid saturation of scarce medical resources, namely intensive care beds and ventilators needed to treat critically-ill patients. In the current study, the simulation of the cumulative number of critical patients indirectly indicated the expected demand of intensive care settings.
The estimation of the total number of infected individuals varied when considering or not asymptomatic patients in the equation. Asymptomatic presentation has been recognized to be between 17.9% and 50.0% ^20-22, and this proportion is steadily increasing as population screening grows. Since population screening was not expected to be implemented in Argentina, all rates were calculated with symptomatic patients, were considered to be infectious in the model.

As of April 22, the cumulative number of symptomatic cases officially reported in the Buenos Aires metropolitan area was 183624. Progression of the quadratic growth curve equation (y = 0.4x.2+36.5 x+22.2) through May 22 would estimate a cumulative number of about 5000 cases for the area, as long as the quarantine is maintained.
This expected growth would coincide with the simulation scenario associated with 40% of the quarantined population. It should be clarified that the compulsory total quarantine does not effectively affect a significant portion of the population, namely, health and basic services staff, and food-related personnel. These exceptions and the contact these people have with quarantined susceptible individuals make an effective isolation rate of around 40%.
Recently, another local simulation analysis for AMBA based on a modeling study of the Wuhan outbreak was reported ^{12, 25}. The authors built a SEIR epidemiological model to explore alternative scenarios like the present study. However, some important differences arose when comparing both models. Based on governmental official figures, Díaz Resquin et al ²⁵ assumed a fixed quarantined susceptible population of 85% of the total population (15% of workforce enabled). Conversely, we considered these figures to be only theoretical, given the family contact between quarantined and non-quarantined individuals, particularly for the healthcare workforce who has the most intimate contact with infected patients and a high probability of contagion. Furthermore, some underserved population of Greater Buenos Aires are in a worse condition to effectively isolate themselves at home. In fact, population compartments are not fixed, since quarantined and nonquarantined people flow with different intensity between the two related compartments (Fig. 1). Díaz Resquin calculated for a non-intervention scenario a peak of 65 000 symptomatic infected people towards the end of August, versus 88 000 cases around the beginning of May for our estimation. That author proposed a series of strategies to exit the lockdown in programmed stages. Regardless of the chosen plan, all the rebounds only appeared from October 2020 to January 2021, just 5 months after the start of the quarantine opening. Our estimates, however, showed immediate new outbreaks, or at most one month after full suspension of the quarantine. This rapid recurrence of the disease is due to exposure and infection of susceptible people coming out of quarantine. Nevertheless, when running our model with higher proportions of quarantined population, the infection curves shifted to the right until October-December (data not shown).
After the first wave of COVID-19, new simulation studies are assessing the impact of a likely second-wave of the epidemic. The potential consequences of anticipating the relaxation of restrictions on the recurrence of infections are now being cause of concern in China and other countries ^26-27. In our study, we also found the development of those new peaks of infection separated and discontinued in time, as in the case of Figure 4c.
A recent systematic review of modeling studies on COVID-19 showed that quarantine could work when it is introduced early alongside other measures28.The study reported that current evidence consistently showed a benefit of isolation measures, with quarantine of people exposed to confirmed or suspected cases averting 44% to 81% incident cases and 31% to 63% of deaths, compared with nomeasures ²⁹. However, only when quarantine was combined with other control measures as school closures, travel restrictions, and social distancing, the models showed a larger effect on the reduction of new cases, and deaths. Anyway, the narrative synthesis of this review has several limitations.
A correlation between universal Bacillus Calmette-Guerin (BCG) vaccination and reduced morbidity and mortality for COVID-19 has been recently proposed to partially explain the different impact of the pandemic in different countries ^{30, 31}. This observation could be related to a recognized non-specific effect of BCG vaccine on viral infections ³². Preliminary studies have shown that countries with long-term implementation of national policies regarding BCG vaccination had a stronger reduction in the number of deaths per million inhabitants in the current pandemic ³³. Though it was not included in the present simulation, this condition should be considered in a future update of the model.
Some comments are pertinent regarding model parameters.
Since Argentina is going through the beginning of the epidemic, there are still scarce local data to calibrate the parameters used in the current estimations. Only the population size and constitution, and the disease-induced death rate were obtained from local information. Like us, other local modelers have applied basic foreign data to implement their simulations ²⁵. Two recent studies have communicated the reduction of the basic reproduction number for Argentina from 1.3 (April 7)³⁴ to 1.0 (April 18) ³⁵. This reduction was rightly considered by the initial parameters of the present model, since the contact rate (c(t)) was calculated as a decreasing function of time.
Thus, the constant contact rate (c) was replaced by a time-dependent coefficient to accurately reflect the evolving public health interventions of Argentina.
Since the current study was carried out at the beginning of the COVID-19 epidemic in Argentina, and we had few local data to calculate the simulation parameters and to validate the model, this could be considered a limitation of the study. Still, current in-advance estimates could be helpful to establish evidence-based public health policies in the context of the present ongoing pandemic. Another limitation is that the simulated cohorts were analyzed as a whole and not divided into age-specific classes reflecting a different risk for acquiring the infection. Asymptomatic or subclinical cases were included in the model, although it is not yet fully proven whether these individuals can transmit or not the infection. Finally, all the outcomes should be considered in the context of widely accepted rational assumptions, and based on the accuracy of the model parameter set obtained from the literature.
In conclusion, we implemented a dynamic simulation model to assess the impact of social distancing on the evolution of the COVID-19 outbreak in the metropolitan area of Buenos Aires. In a low-intervention scenario, the model estimated a maximum peak of nearly 90 000 symptomatic cases for early May. Only mandatory quarantine was able to delay the maximum peak of infection and significantly reduce the total number of infected individuals and deaths at a 150-day term. The interruption of the quarantine before 120 days of its beginning could generate an even more serious outbreak 30 days later, and surpass the scarce medical resources available for the intensive care of critically-ill patients. Although the validation of the current model can only be established in the future, for the moment it will serve as a decision-making tool for public health policies in the context of the present ongoing epidemic in Argentina.

Conflicts of interest: None declared

References

1. Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet 2020; 395: 689-97.
2. Rodriguez-Morales AJ, Gallego V, Escalera-Antezana JP, et al. COVID-19 in Latin America: The implications of the first confirmed case in Brazil. Travel Med Infect Dis 2020; 101613. doi: 10.1016/j.tmaid.2020.101613.
3. Wu Z, McGoogan JM. Characteristics of and Important Lessons From the Coronavirus Disease 2019 (COVID-19) Outbreak in China: Summary of a Report of 72 314 Cases From the Chinese Center for Disease Control and Prevention. JAMA 2020. doi:10.1001/jama.2020.2648
4. Hellewell J, Abbott S, Gimma A, et al. Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group, Funk S, Eggo RM. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob Health 2020. doi:10.1016/S2214-109X(20)30074-7
5. Kucharski AJ, Russell TW, Diamond C, et al. Centre for Mathematical Modelling of Infectious Diseases COVID-19 working group. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis 2020; S1473-3099(20)30144-4. doi: 10.1016/S1473-3099(20)30144-4
6. Tang SY, Xiao YN, Peng ZH, Shen HB. Prediction modeling with data fusion and prevention strategy analysis for the COVID-19 outbreak. Zhonghua Liu Xing Bing Xue Za Zhi 2020; 41: 480-4.
7. Fang Y, Nie Y, Penny M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions: A data-driven analysis. J Med Virol 2020; 06: 06.
8. Tang B, Bragazzi NL, Li Q, Tang S, Xiao Y, Wu J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect Dis Model 2020; 5: 248-55.
9. Fu X, Ying Q, Zeng T, Long T, Wang Y. Simulating and forecasting the cumulative confirmed cases of SARSCoV-2 in china by Boltzmann function-based regression analyses. J Infect 2020. pii: S0163-4453(20)30098-0. doi: 10.1016/j.jinf.2020.02. 019.
10. Choi SC, Ki M. Estimating the reproductive number and the outbreak size of Novel Coronavirus disease (COVID-19) using mathematical model in Republic of Korea. Epidemiol Health 2020; e2020011.
11. Lin Q, Zhao S, Gao D, et al. A conceptual model for the outbreak of Coronavirus disease 2019 (COVID-19) in Wuhan, China with individual reaction and governmental action. Int J Infect Dis 2020. pii: S1201-9712(20)30117-X.doi: 10.1016/j.ijid.2020. 02.058
12. Prem K, Liu Y, Russell TW, Kucharski AJ, Eggo RM, Davies N; Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group, et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health 2020. pii: S2468-2667(20)30073-6. doi: 10.1016/S2468-2667(20)30073-6
13. Editorial. COVID-19: learning from experience. Lancet 2020; 395: 1011.
14. Bedford J, Enria D, Giesecke J, et al. COVID-19: towards controlling of a pandemic. Lancet 2020; 395: 1015-8.
15. Mahase E. Covid-19: UK starts social distancing after new model points to 260 000 potential deaths. BMJ 2020; 368: m1089.
16. Tang B, Wang X, Li Q, et al. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J Clin Med 2020; 9: 462.
17. Censo nacional de población, hogares y viviendas 2010: censo del Bicentenario: resultados definitivos, Serie B nº 2. – 1a ed. – Buenos Aires: Instituto Nacional de Estadística y Censos – INDEC, 2012.
18. Basic indicators, Argentina. Ministerio de Salud de la Nación. Pan American Health Organization – PAHO/WHO, 2016. In: http://www.paho.org/arg; accessed March 2020.
19. Backer JA, Klinkenberg D, Wallinga J. The incubation period of 2019-nCoV infections among travellers from Wuhan, China. medRxiv 2020. doi: 10.1101/2020.01.27.20018986
20. Mizumoto K, Kagaya K, Zarebski A, Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Euro Surveill 2020, 25:pii=2000180. doi: 10.2807/ 1560-7917
21. Nishiura H, Kobayashi T, Suzuki A, et al. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19). Int J Infect Dis 2020. pii: S1201-9712(20)30139-9. doi: 10.1016/.ijid.2020.03.020
22. Day M. Covid-19: identifying and isolating asymptomatic people helped eliminate virus in Italian village. BMJ 2020; 368: m1165.
23. Emanuel EJ, Persad G, Upshur R, et al. Fair Allocation of Scarce Medical Resources in the Time of Covid-19. N Engl J Med 2020 Mar 23. doi: 10.1056/NEJMsb2005114
24. Ministerio de Salud de la Nación. Situación de COVID-19 en Argentina. Reporte diario matutino Nro 79 (23/4/2020). In: https://www.argentina.gob.ar/coronavirus/informediario; accessed April 2020.
25. Díaz Resquin MC, Ascolani J, Díaz CA, Díaz Martirena FH, Lighuen PM. Modelación Matemática de la propagación del COVID-19: Área Metropolitana de Buenos Aires (AMBA), Argentina. In: https://saludbydiaz.com/2020/04/08/ modelacion-matematica-de-la-propagacion-del-covid-19-area-metropolitana-de-buenos-airesamba/; accessed April 2020.
26. Leung K, Wu J T, Liu D, Leung GM. First-wave COVID-19 transmissibility and severity in China outside Hubei after control measures, and second-wave scenario planning: a modelling impact assessment. Lancet 2020; published online April 8. https://doi.org/ 10.1016/S0140-6736(20)30746-7.
27. Xu S, Li Y. Beware of the second wave of COVID-19. Lancet 2020; published online April 2. org/10.1016/S0140-6736(20)30845-X
28. Mahase E. Covid-19: Quarantine works when introduced early alongside other measures, finds review. BMJ 2020; 369: m1450.
29. Nussbaumer-Streit B, Mayr V, Dobrescu AI, et al. Quarantine alone or in combination with other public health measures to control COVID-19: a rapid review. Cochrane Database Syst Rev 2020; 4: CD013574.
30. Sala G, Miyakawa T. Association of BCG vaccination policy with prevalence and mortality of COVID-19. medRxiv 2020.03.30.20048165; doi: https://doi.org/10.1101/2020.03.30.20048165
31. Shet A, Ray D, Malavige N, Santosham M, Bar-Zeev N. Differential COVID-19-attributable mortality and BCG vaccine use in countries. medRxiv 2020.04.01.20049478; doi: https://doi.org/10.1101/2020.04.01.20049478
32. Moorlag SJCFM, Arts RJW, van Crevel R, Netea MG. Non-specific effects of BCG vaccine on viral infections. Clin Microbiol Infect 2019; 25, 1473-8.
33. Miller A, Reandelar MJ, Fasciglione K, Roumenova V, Li Y, Otazu GH. Correlation between universal BCG vaccination policy and reduced morbidity and mortality for COVID-19: an epidemiological study. medRxiv 2020.03.24.20042937; doi: https://doi.org/10.1101/2020.03.24.20042937
34. Andrino B, Grasso D, Llaneras K. Así evoluciona la curva del coronavirus en México, Colombia, Chile, Argentina y España. El País, España. 7/4/2020. In: https://elpais.com/sociedad/2020/04/13/actualidad/1586788600_ 290634.html; accessed April 2020.
35. Marcelo Beltrán. Evolución del COVID-19 en la Argentina al 18/4… y después. 23/4/2020. In: https://www.medicinabuenosaires.com/evolucion-del-covid-19-en-la-argentinaal-18-4y-despues/; accessed April 2020.